我们要定义一个函数(或者说一个事件新的属性,称为自信息),该函数能够衡量当一件事情在发生之前事件的不确定性,如此我们首先达成以下共识:
- 事件需要依据它的固有属性数字化,这里我们使用事件发生的概率
- 当一个事件发生的概率越大,所含信息量越少,概率为1时候,信息量为0。
- 独立事件同时发生时候,信息量是各个独立事件信息量之和
- 事件发生概率的微小变动会影响自信息
注意,这里的信息量是一种信息容量,就像kg一样刻画物体的质量,但是不同的是,信息容量表示的内在含义是指数级的,如3bit相对于1bit,数字上是3倍,但是3bit可以刻画的状态数却是四倍于1bit。我们可以粗浅理解这里的信息量类似于比特数,它是一种新的量纲!
1 数学描述
Cond1
设事件 属于一个给定的事件集合(空间),其发生概率为:
因此我们要找一个实函数,其性质如下:
Cond2
该函数是一个单调递减函数:
并且有一个固定点:
Cond3
独立事件同时发生的概率等于各个事件发生概率之积,因此函数具有以下性质:
Cond4
是一个连续的函数
2 数学证明
2.1 提出命题
满足上述四个条件的函数只能是:
其中c是一个正实数,b是一个任何大于1的整数。
2.2 证明过程
2.2.1 引理-1
先证明如下引理:对于
证明:
当n=1时,根据Cond2,左,右左,等式成立。
当n>1时,依据公式1-1以及公式1-2,知道当n<m时,
同时,依据公式1-2,不难推导出对于任意非负整数k,有:
对于任意正整数r,一定有非负整数k:
根据公式1-1和公式2-3以及且:
易知:
综合公式2-4和公式2-5有:
因为b也是常量,当n固定时候,,可以知道:
引理-1得证。
2.2.2 引理-2
再证明如下引理:对于正有理数,有:
其中是一个常数。
证明:因为p是一个正有理数,所以一定存在正整数r,s使得。
由公式1-2知:
根据中间引理-1知:
所以中间引理-2得证。
2.2.3 引理-3
最后证明如下引理:
函数连续 易知:
所以连续得证。
综合上述3个引理,原命题得证。
补充
我们通常将c设置为1,对于不同底数b,单位是不同的,b=2时,单位为bit,b=e也就是自然底数时,单位为nat
※ Entrophy
自信息讨论的是一整个事件空间中某一个事件的属性,这个属性只依赖于事件发生的概率。
可以这样理解:所谓自信息,香农提出的是概率性度量,香农认为,记录一个概率发生小的事件比概率发生大的事件需要更多的空间,因为一个人确定低概率事件发生所需要的不确定性代价更高。这符合直觉吗?联想一下哈夫曼编码,当我们给大概率事件赋予更少比特数时候,压缩率达到最高。
1 熵的定义
对于一个概率质量函数为离散随机变量,它的熵定义为:或者:
其中是随机变量取值的有限大小的字母集合,熵的含义是:当了解到字母集合中一个字母出现时候,一个人能够获得信息量的的统计均值。
在计算熵的时候我们规定:
因为随着,
特别的,对于一个服从分布的随机变量,如果,并且,是一个定值,那么:
2 熵的属性
2.1 Fundamental Inequality(FI)
对于任意,,下面的不等式:
成立,且等号当且仅当时成立
令代入上式,亦得:
对于任意成立,并且等号当且仅当时成立。
2.2 Nonenegativity
恒成立,且等号当且仅当X是确定性的时候成立。
2.3 Upper bound on entropy
如果随机变量从一个有限字母集合中取值,那么无论随机变量的概率分布如何,它的熵有一个上界:
其中表示字母集合的大小,等号当且仅当服从均匀分布成立。这个上界还叫Hartley's function or entrophy
2.4 Log-sum inequlity
对于所有非负数,和,有不等式:
等式当且仅当对于所有的,
证明可以使用著名的琴生不等式加权版(Jensen's inequality)。
凸集
一个集合是凸集(convex set),如果对任意和 都有:
仿射集自然是凸集的一种,类比于仿射集的相关概念,我们可以得到凸包(convex hull )的定义:
严格凸函数
如果定义域是凸集,有有:
成立,且当且时候,上述不等式不等号严格成立,则称为严格凸函数。
📌琴生不等式
对于任何严格凸函数(strictly convex function),如果并且,则:
成立,且等号当且仅当
3 联合熵和条件熵
回顾条件概率,这里千万记住:的含义是也就是,在发生的条件下,一起发生的概率。
同理,的含义是也就是,在均发生的条件下 发生的概率。
总之,''左右是一个整体,','的运算优先级高于 ''
3.1 二维元素事件的自信息
一对随机变量,其联合概率质量函数为,则对于元事件,其自信息为:
3.2 联合熵的定义
随机变量的熵定义为:
3.3 条件熵的定义
给定两个联合分布的随机变量,考虑对于的条件熵定义为:
3.4 定理和推论
熵的链式法则
由联合熵的定义知:,具有可交换性。所以:
进一步有:
上面等式中两边的含义就是后面会介绍的互信息(mutual information)!
条件熵的链式法则
通俗理解,就是熵的链式法则的推广,只不过熵的链式法则是在全局事件空间下,
而条件熵则是在局部事件空间中。
4 联合熵和条件熵的属性
4.1 条件不增性 Conditioning never increases entrophy
引入条件后,事件空间不确定性不可能增加,可以认为产生了信息增益:
当且仅当独立时候取等。
4.2 独立可加性 Additivive for independent random variables
对于相互独立的随机变量,其联合熵可以表示为:
4.3 条件不等式 Conditional entrophy is lower additive
1 互信息的定义
通俗理解:对于两个随机变量和,当观察到某一个随机变量时候,另一个随机变量不确定性减少的量。很显然,由定义容易推断其有对称性。事实上,它就隐藏在上一章熵的链式法则中:
2 互信息的属性
2.1 互信息的等价表达式
上述三个等式都可以根据熵的定义容易推出。
2.2 互信息不大于单随机变量的熵
等号当且仅当对于一些情况成立。
2.3 互信息非负性
等号当且仅当和相互独立。
2.4 互信息的上界
这可以根据互信息的定义式以及熵的上界不等式推出。
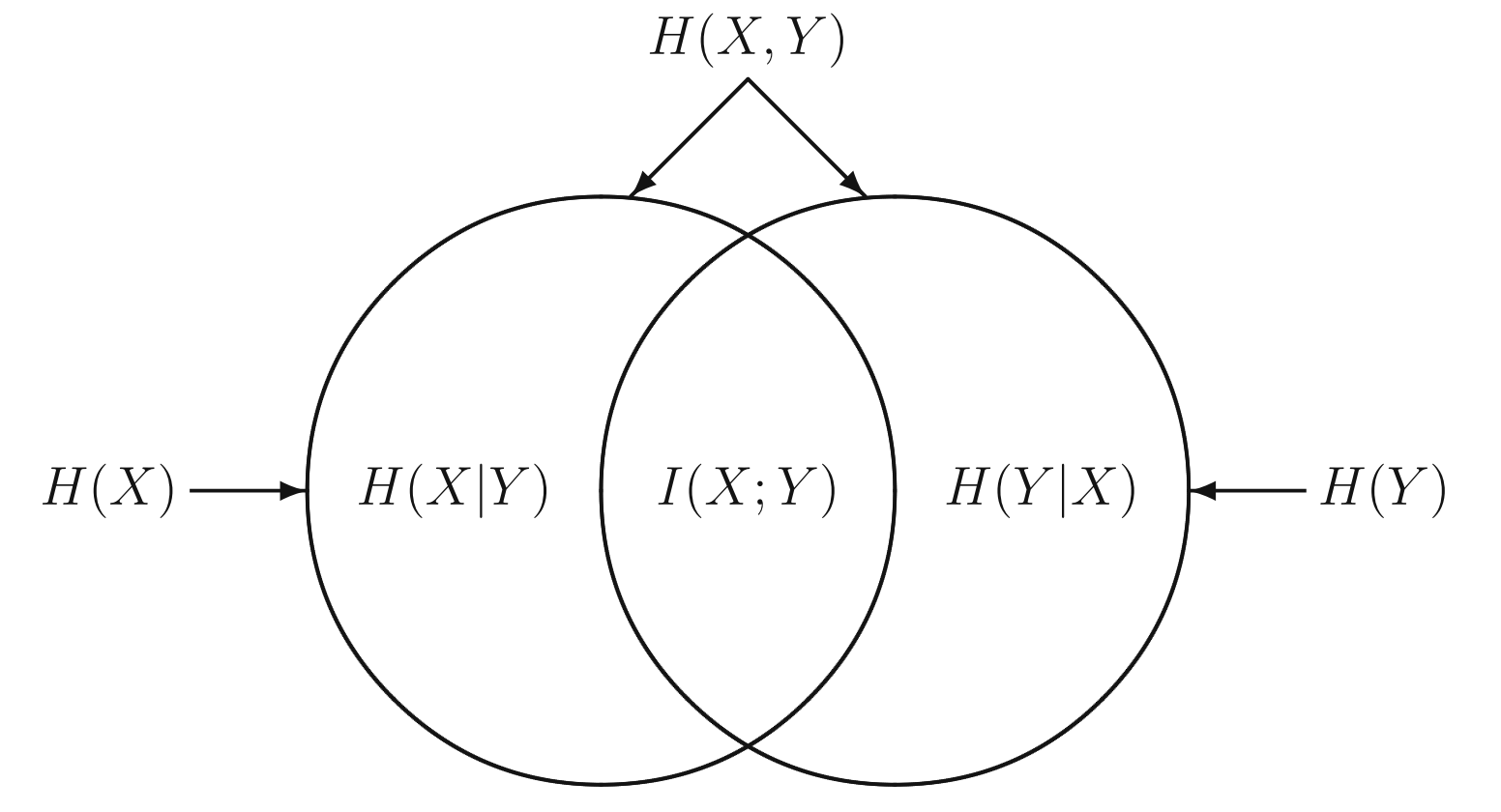
熵,条件熵,联合熵,之间的Venn图关系如下:
3 条件互信息
注意:在中,关系运算符的优先级从高到低是
3.1 定义
在获取了知识情况下,随机变量和之间的共享不确定性。
3.2 联合互信息和互信息的链式法则
定义随机变量和联合随机变量联合互信息:
我们有链式法则如下:
使用Venn图理解就是:
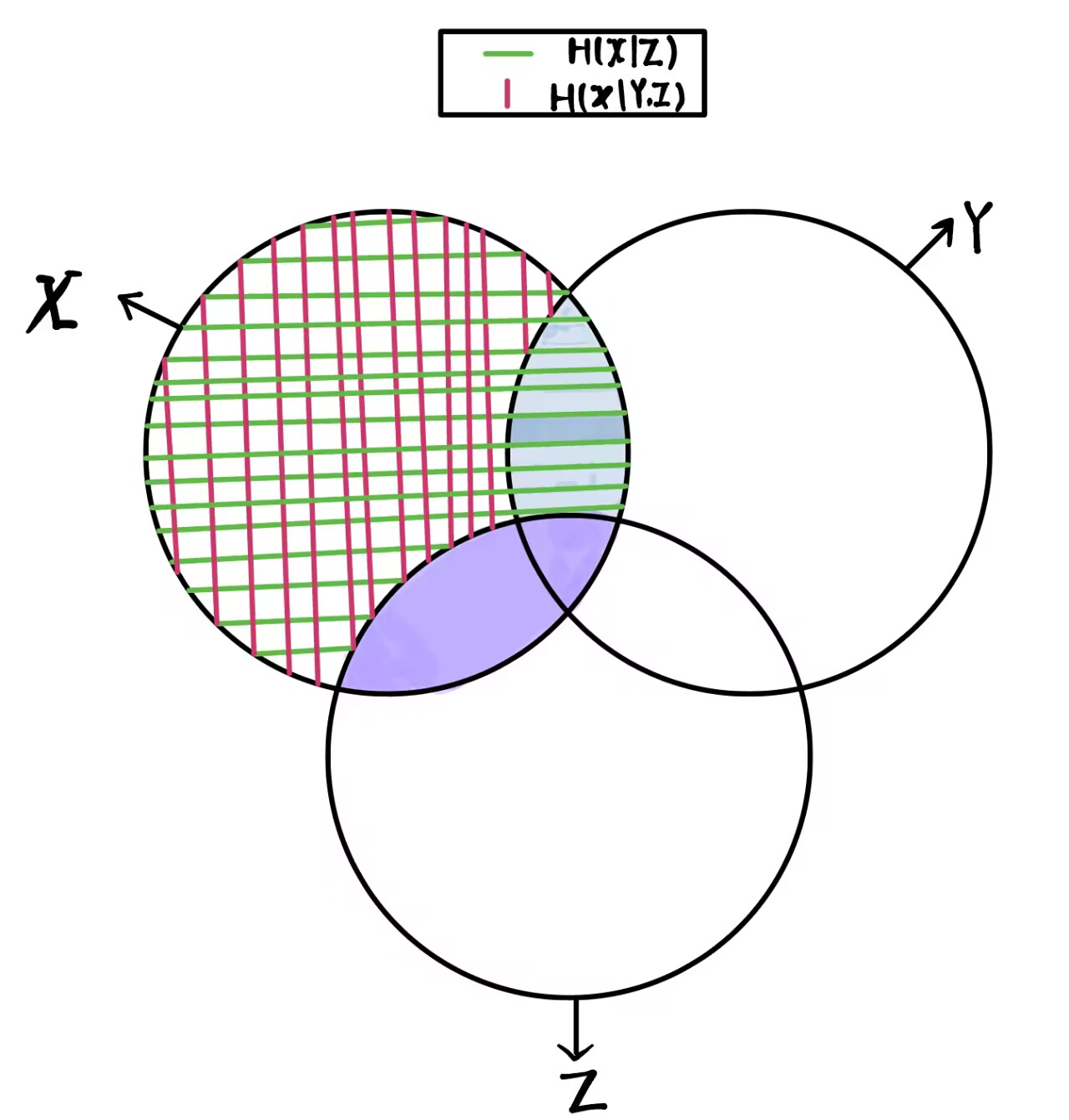
其中上图图紫色实心区域为:,蓝色实心区域为:。而链式法则第二个等号右侧的含义就是 紫色实心区域 + 蓝色实心区域 得到随机变量与联合分布之间的互信息:
参考链接🔗
1. No.2 信息熵的广义可加性:条件熵、互信息的几何含义 - 知乎 (zhihu.com)
2. No.3 梳理汇总:信息熵、条件熵和互信息的性质及其推导 - 知乎 (zhihu.com)
3. 琴生不等式(Jensen's inequality)的证明 - 知乎 (zhihu.com)
4. Convex function - 知乎 (zhihu.com)

